Examples
The vector space R3 has
as a basis, and therefore we have dimR(R3) = 3. More generally, dimR(Rn) = n, and even more generally, dimF(Fn) = n for any field F.
The complex numbers C are both a real and complex vector space; we have dimR(C) = 2 and dimC(C) = 1. So the dimension depends on the base field.
The only vector space with dimension 0 is {0}, the vector space consisting only of its zero element.
Facts
If W is a linear subspace of V, then dim(W) ≤ dim(V).
To show that two finite-dimensional vector spaces are equal, one often uses the following criterion: if V is a finite-dimensional vector space and W is a linear subspace of V with dim(W) = dim(V), then W = V.
Rn has the standard basis {e1, ..., en}, where ei is the i-th column of the corresponding identity matrix. Therefore Rn has dimension n.
Any two vector spaces over F having the same dimension are isomorphic. Any bijective map between their bases can be uniquely extended to a bijective linear map between the vector spaces. If B is some set, a vector space with dimension |B| over F can be constructed as follows: take the set F(B) of all functions f : B → F such that f(b) = 0 for all but finitely many b in B. These functions can be added and multiplied with elements of F, and we obtain the desired F-vector space.
An important result about dimensions is given by the rank-nullity theorem for linear maps.
If F/K is a field extension, then F is in particular a vector space over K. Furthermore, every F-vector space V is also a K-vector space. The dimensions are related by the formula
- dimK(V) = dimK(F) dimF(V).
In particular, every complex vector space of dimension n is a real vector space of dimension 2n.
Some simple formulae relate the dimension of a vector space with the cardinality of the base field and the cardinality of the space itself. If V is a vector space over a field F then, denoting the dimension of V by dimV, we have:
- If dim V is finite, then |V| = |F|dimV.
- If dim V is infinite, then |V| = max(|F|, dimV).
Generalizations
One can see a vector space as a particular case of a matroid, and in the latter there is a well defined notion of dimension. The length of a module and the rank of an abelian group both have several properties similar to the dimension of vector spaces.
The Krull dimension of a commutative ring, named after Wolfgang Krull (1899–1971), is defined to be the maximal number of strict inclusions in an increasing chain of prime ideals in the ring.
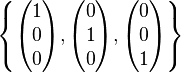

Tidak ada komentar:
Posting Komentar