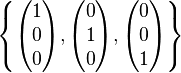Dimension (vector space)

In mathematics, the dimension of a vector space V is the cardinality (i.e. the number of vectors) of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension. All bases of a vector space have equal cardinality (see dimension theorem for vector spaces) and so the dimension of a vector space is uniquely defined. The dimension of the vector space V over the field F can be written as dim_F(V) or as [V : F], read "dimension of V over F". When F can be inferred from context, often just dim(V) is written.

Examples

The vector space R³ has

as a basis, and therefore we have dim_R(R³) = 3. More generally, dim_R(Rⁿ) = n, and even more generally, dim_F(Fⁿ) = n for any field F.

The complex numbers C are both a real and complex vector space; we have dim_R(C) = 2 and dim_C(C) = 1. So the dimension depends on the base field.

The only vector space with dimension 0 is {0}, the vector space consisting only of its zero element.

Facts

If W is a linear subspace of V, then dim(W) ≤ dim(V).

To show that two finite-dimensional vector spaces are equal, one often uses the following criterion: if V is a finite-dimensional vector space and W is a linear subspace of V with dim(W) = dim(V), then W = V.

Rⁿ has the standard basis {e₁, ..., e_n}, where e_i is the i-th column of the corresponding identity matrix. Therefore Rⁿ has dimension n.

Any two vector spaces over F having the same dimension are isomorphic. Any bijective map between their bases can be uniquely extended to a bijective linear map between the vector spaces. If B is some set, a vector space with dimension |B| over F can be constructed as follows: take the set F^(B) of all functions f : B → F such that f(b) = 0 for all but finitely many b in B. These functions can be added and multiplied with elements of F, and we obtain the desired F-vector space.

An important result about dimensions is given by the rank-nullity theorem for linear maps.

If F/K is a field extension, then F is in particular a vector space over K. Furthermore, every F-vector space V is also a K-vector space. The dimensions are related by the formula

dim_K(V) = dim_K(F) dim_F(V).

In particular, every complex vector space of dimension n is a real vector space of dimension 2n.

Some simple formulae relate the dimension of a vector space with the cardinality of the base field and the cardinality of the space itself. If V is a vector space over a field F then, denoting the dimension of V by dimV, we have:

If dim V is finite, then |V| = |F|^dimV.

If dim V is infinite, then |V| = max(|F|, dimV).

Generalizations

One can see a vector space as a particular case of a matroid, and in the latter there is a well defined notion of dimension. The length of a module and the rank of an abelian group both have several properties similar to the dimension of vector spaces.

The Krull dimension of a commutative ring, named after Wolfgang Krull (1899–1971), is defined to be the maximal number of strict inclusions in an increasing chain of prime ideals in the ring.

dimension

In mathematics, the dimension of a space is roughly defined as the minimum number of coordinates needed to specify every point within it[1][2]. For example: the circle in the plane can be described by two Cartesian coordinates but one can make do with less (the polar coordinate angle), thus a circle is 1-dimensional even though it exists in the 2-dimensional plane. This intrinsic notion of dimension is one of the chief ways in which the mathematical notion of dimension differs from its common usages.

There is also an inductive description of dimension: consider a discrete set of points (such as a finite collection of points) to be 0-dimensional. By dragging a 0-dimensional object in some direction, one obtains a 1-dimensional object. By dragging a 1-dimensional object in a new direction, one obtains a 2-dimensional object. In general one obtains an n+1-dimensional object by dragging an n dimensional object in a new direction. Returning to the circle example: a circle can be thought of as being drawn as the end-point on the minute hand of a clock, thus it is 1-dimensional. To construct the plane one needs two steps: drag a point to construct the real numbers, then drag the real numbers to produce the plane.

Consider the above inductive construction from a practical point of view -- ie: with concrete objects that one can play with in one's hands. Start with a point, drag it to get a line. Drag a line to get a square. Drag a square to get a cube. Any small translation of a cube has non-trivial overlap with the cube before translation, thus the process stops. This is why space is said to be 3-dimensional.

High-dimensional spaces occur in mathematics and the sciences for many reasons, frequently as configuration spaces such as in Lagrangian or Hamiltonian mechanics. Ie: these are abstract spaces, independent of the actual space we live in. The state-space of quantum mechanics is an infinite-dimensional function space. Some physical theories are also by nature high-dimensional, such as the 4-dimensional general relativity and higher-dimensional string theories.
In mathematics, the dimension of Euclidean n-space E n is n. When trying to generalize to other types of spaces, one is faced with the question “what makes E n n-dimensional?" One answer is that in order to cover a fixed ball in E n by small balls of radius ε, one needs on the order of ε−n such small balls. This observation leads to the definition of the Minkowski dimension and its more sophisticated variant, the Hausdorff dimension. But there are also other answers to that question. For example, one may observe that the boundary of a ball in E n looks localy like E n − 1 and this leads to the notion of the inductive dimension. While these notions agree on E n, they turn out to be different when one looks at more general spaces.

A tesseract is an example of a four-dimensional object. Whereas outside of mathematics the use of the term "dimension" is as in: "A tesseract has four dimensions," mathematicians usually express this as: "The tesseract has dimension 4," or: "The dimension of the tesseract is 4."

Although the notion of higher dimensions goes back to Rene Descartes, substantial development of higher-dimensional geometry only began in the 19th century, via the work of Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli and Bernhard Riemann. Riemann's 1854 Habilitationsschrift, Schlafi's 1852 Theorie der vielfachen Kontinuität, Hamilton's 1843 discovery of the quaternions and the construction of the Cayley Algebra marked the beginning of higher-dimensional geometry.

The rest of this section examines some of the more important mathematical definitions of dimension.